球面三角と打ち上げ方位

ロケット・宇宙船の打ち上げ方位を計算する以下の公式について、簡単に説明します。

\begin{equation*} 打ち上げ方位=\arcsin \left( \frac {\cos (ターゲットの軌道傾斜角)}{\cos (打ち上げ地点の緯度)}\right) \end{equation*}

三角形を描く

打ち上げ地点を通り、両極を結ぶ線（子午線）
赤道
ターゲットの軌道面

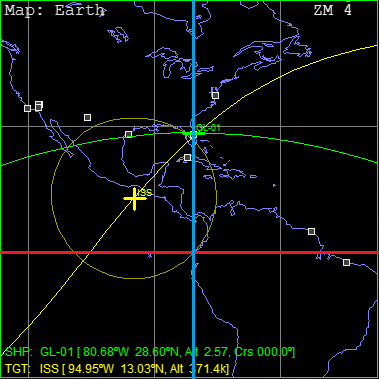
青が子午線、赤が赤道、黄色がターゲットの軌道面。
（緑は自機を真東に打ち上げたときの軌道面だが、今回は無関係）

これら3つの線が交差するところに、三角形を描くことができる。
子午線とターゲットの軌道面（青と黄色）がつくる角度が、打ち上げ方位ということになる。

この三角形について、以下の情報が明らかになっている。

打ち上げ地点の緯度
ターゲットの軌道傾斜角（赤道に対しての軌道面の角度）
子午線と赤道が交差する角度（＝直角）

内角2つ（軌道傾斜角と、子午線と赤道が交差する角度）がわかっている。
しかし球面上の三角形では、内角の和は180°から540°までの値を取る。※
このため、球面三角法の公式を使って3つ目の内角を求める必要がある。

※球面三角形の内角の和
$$ 180^\circ \lt \theta \lt 540^\circ $$

球面三角形の定義

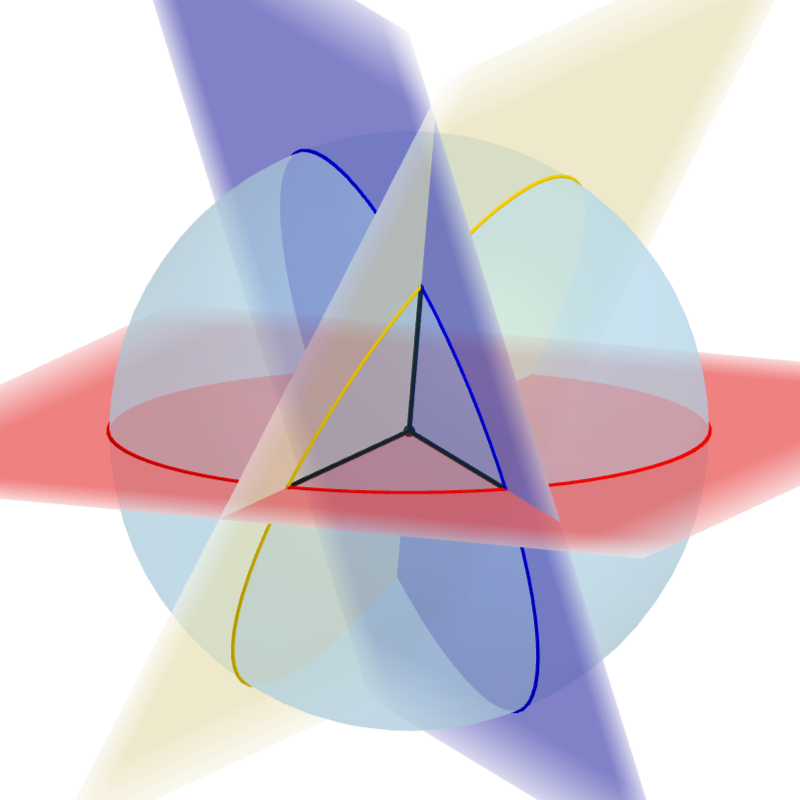
球の中心を通る3つの平面を考える。
それぞれの平面が球の表面と交差してできる円を大円と呼ぶ。
3つの大円の弧で構成される図形が球面三角形である。

球面三角形の内角は、これら3つの平面のなす角として定義される。
例えば軌道傾斜角は、赤道面（もしくは黄道面）と衛星の軌道平面のなす角である。

直角球面三角形の公式

3つの角をA, B, C、各辺をa, b, cとする。

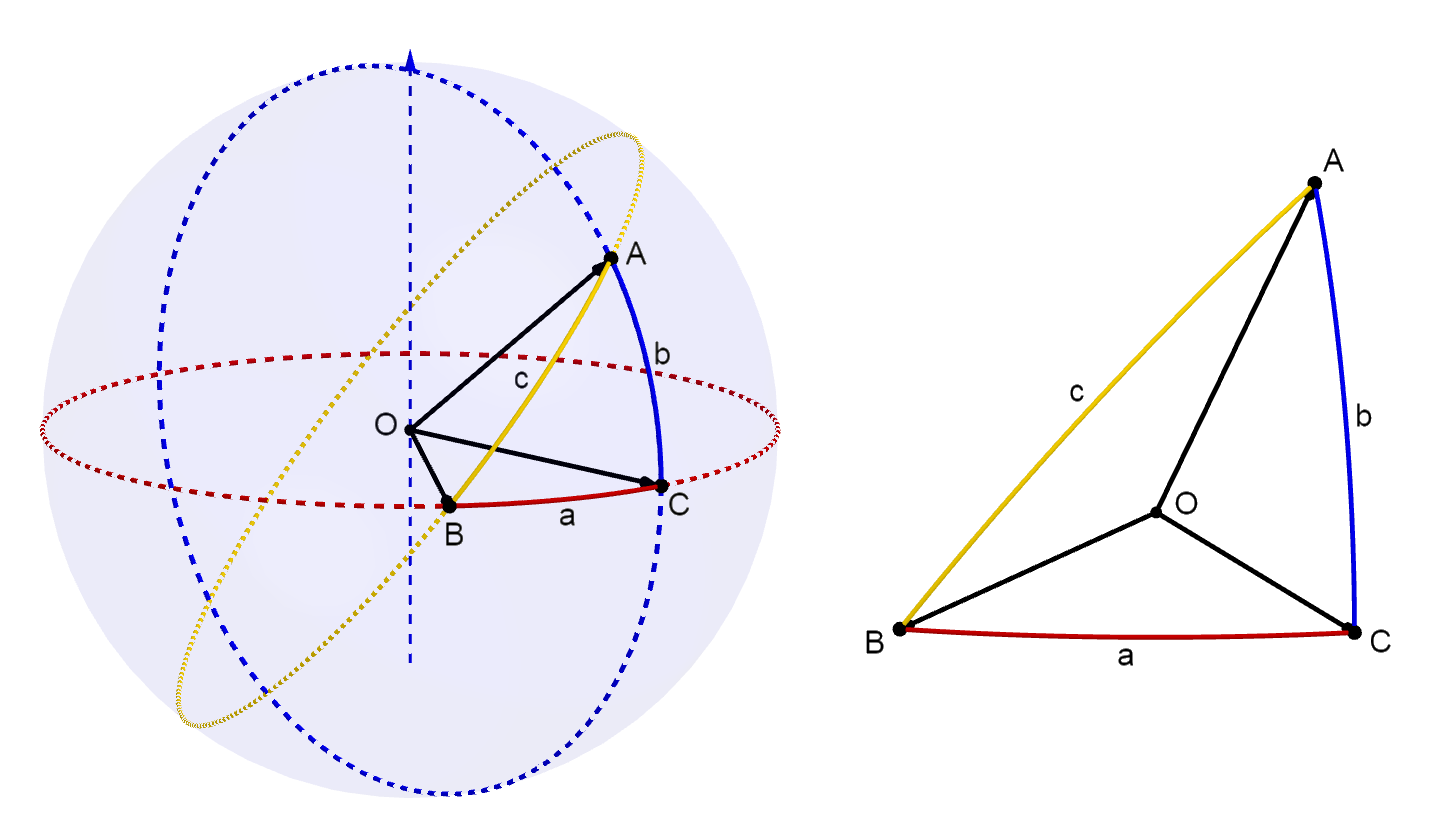
球の半径を1とすると、辺a, b, cの長さを角度で表すことができる。
例えば、赤道から打ち上げ地点までの子午線の長さは緯度で表すことができる。

また、辺bは子午線の一部であるため、角Cが直角であることがわかっている。

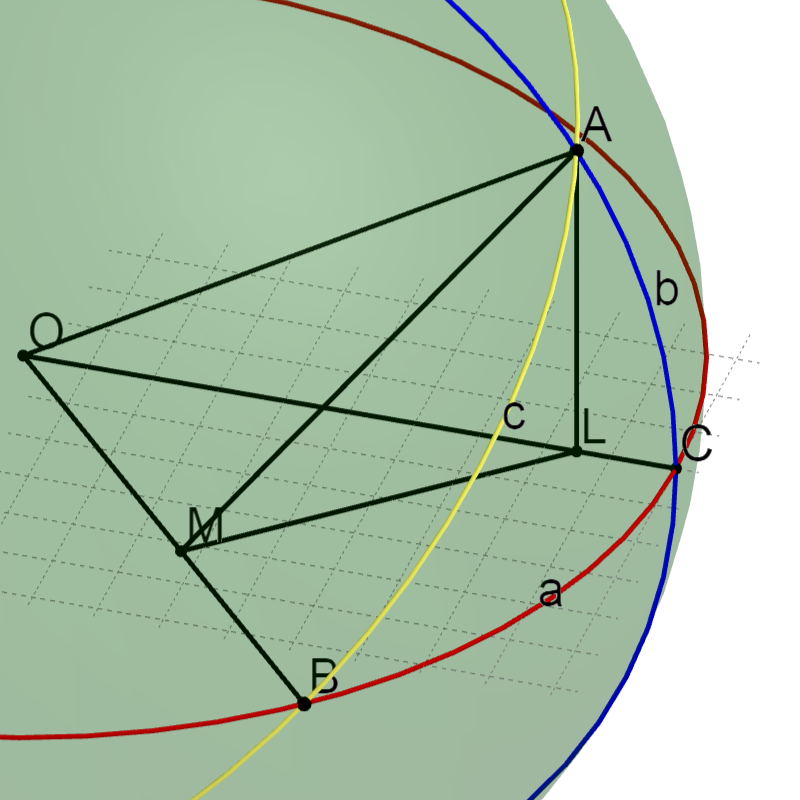
点AからOCに垂線を下ろし、交点をLとする。
点AからOBに垂線を下ろし、交点をMとする。

\begin{align} AL &= \sin b \notag \\ AM &= \sin c \notag \end{align}

LとMを結ぶ直線を引く。
三垂線の定理より、LMはOBに対して垂直であるため、∠AMLはBに等しい。
したがって、

\begin{align} AM \sin B &= AL \notag \\ \sin c \sin B &= \sin b \notag \end{align}

Aおよびaについても同様に、

\begin{equation} \sin c \sin A = \sin a \end{equation}

また、AMおよびOLと、LMのあいだには以下のような関係がある。

\begin{align} AM \cos B &= LM \notag \\ \sin c \cos B &= LM \notag \\ \notag \\ OL &= \cos b \notag \\ OL \sin a &= LM \notag \\ \cos b \sin a &= LM \notag \end{align}

したがって、

\begin{align} \sin c \cos B &= \cos b \sin a \\ \sin c \cos A &= \cos a \sin b \notag \end{align}

(1)および(2)より、

\begin{align} \sin A &= \frac {\cos B} {\cos b} \notag \\ A &= \arcsin \left( \frac {\cos B} {\cos b} \right) \notag \end{align}

緯度と軌道傾斜角

$ \arcsin x $ の定義域は、$ -1 \leqq x \leqq 1 $ である。
打ち上げ地点の緯度が軌道傾斜角より大きいとき、cos(軌道傾斜角)/cos(緯度)の商は1より大きくなる。
したがって、緯度が軌道傾斜角より大きいとき、上記の式を使って打ち上げ方位を決めることはできない。

このような場合は、いったん軌道上に出てから軌道面を一致させるか、Off-plane transferを実行する。

打ち上げ方位を計算する

参考文献

長谷川一郎，1996，『天文計算入門』恒星社厚生閣